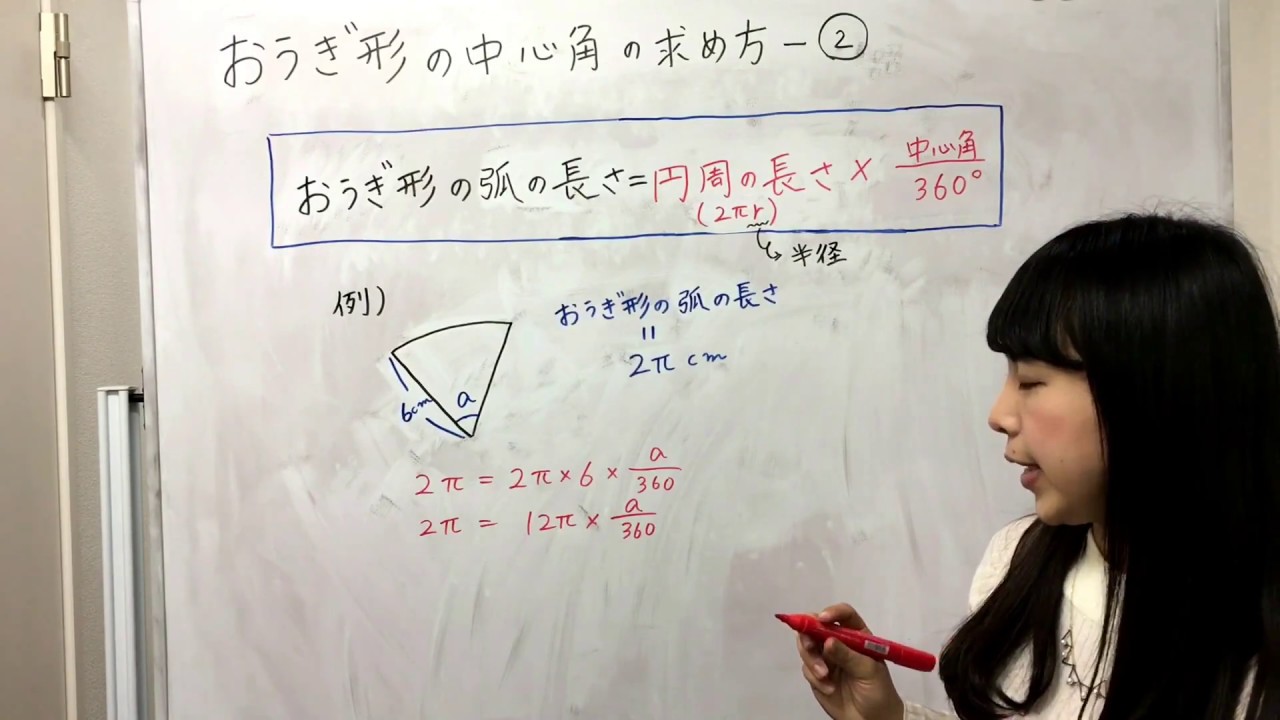
以下のおうぎ形について中心角を求めなさい。(ただし円周率は314とします。) (1)半径10cmで弧の長さが157cm 基本的な解き方 「半径が等しいおうぎ形のポイント」を利用した解き方 360×157/628=90 答え 90 ° 工夫した解き方おうぎ形弧の長さ・面積・中心角の求め方 年10月23日 学習内容解説ブログサービスリニューアル・受験情報サイト開設のお知らせ 学習内容解説ブログをご利用下さりありがとうございます。半径3cm,中心角1°のおうぎ形の面積と弧の長さを求めなさい。 問題の見方 半径と中心角を,おうぎ形の公式に代入して求めましょう。 この公式が覚えづらい人は,おうぎ形が円の一部だということを意識しましょう。
 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式" />
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式" /> 作図 角度15 30 45 60 75 90 105 の作り方を解説 数スタ
おうぎ形 中心角 求め方 公式
おうぎ形 中心角 求め方 公式-以下のおうぎ形について中心角を求めなさい。(ただし円周率は314とします。) (1)半径10cmで弧の長さが157cm 基本的な解き方 「半径が等しいおうぎ形のポイント」を利用した解き方 360×157/628=90 答え 90 ° 工夫した解き方数学・算数 扇形の中心角は 初めまして^^ 私はこの前インフルエンザで休んでいて、扇形の中心角など、空間図形や平面図形の求め方がイマイチ理解していないような気がします。 なので、扇形の中心角を中心 質問No
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1数学 円すいの問題 練習編 映像授業のtry It トライイット
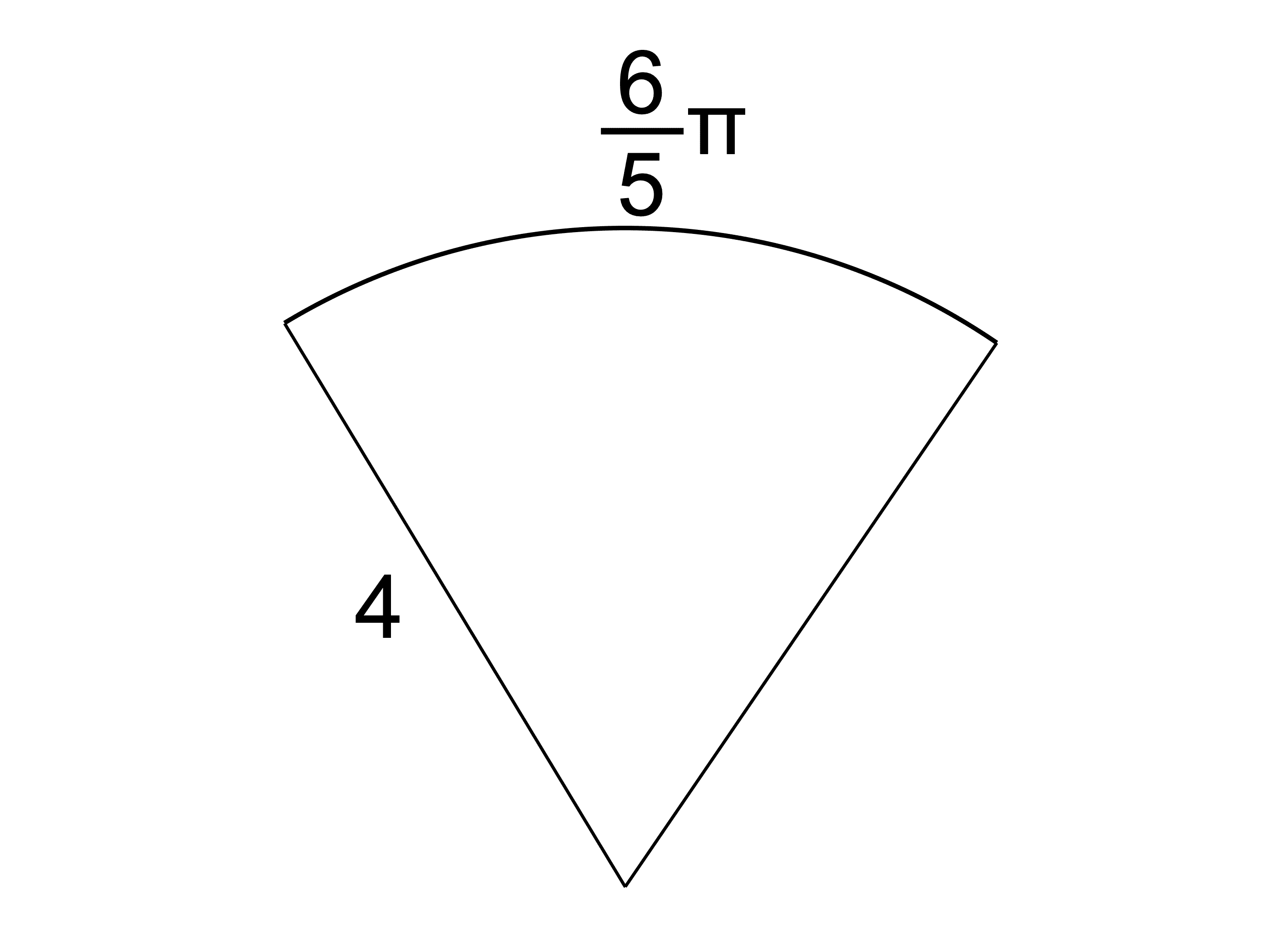
中心角の求め方は2通りのパターンがあります。 中1のおうぎ形の中心角の求め方の公式を教えてください。 裏技ではなく、学校で習う方式の方がありがたいですが、やっても良い裏技があれば二種類お願いします。 1半径が3cm、弧の長さが3πcmのおうぎ形念のために、 公式に頼らない「扇形の中心角の求め方」 をみていこう。 さっきの「半径4cm、弧の長さ6π cmの扇形」の中心角を求めてみるよ。 中心角はつぎの3ステップで計算できるんだ。 問題 (1) 半径が 3cm、弧の長さが 3π cm のおうぎ形の中心角を求めおうぎ形の中心角の求め方と公式 中心角 問題 (1) 半径が 3cm、弧の長さが 3π cm のおうぎ形の中心角を求めなさい。 (2) 半径が 4cm、弧の長さが π cm のおうぎ形の中心角を求めなさい。 (3) 半径が 2cm、弧の長さが π/2 cm のおうぎ形の中心角を求めなさい。
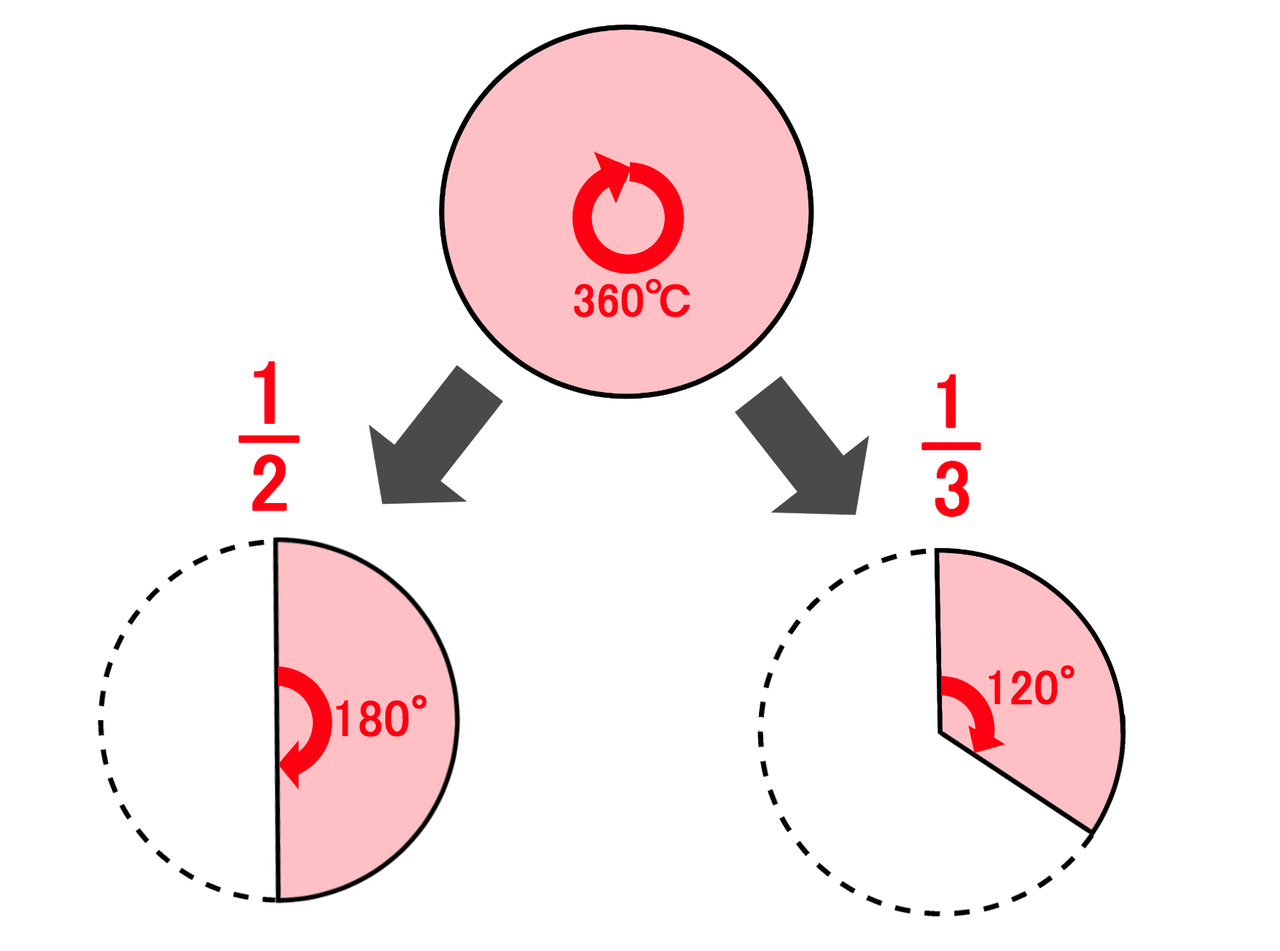
この2つさえ覚えていれば、中心角を求めるだけじゃなくて 面積や弧の長さを求める問題にも対応できるようになるよ じゃあ、具体的に見ていこうね 具体的に解く 中心角の求め方の問題は3パターン考えられるよ 弧の長さと半径が分かっている場合おうぎ形の弧の長さと面積の求め方|小学生に教えるための解説 今回はおうぎ形の弧の長さや面積の公式や問題の解き方について解説していき、おうぎ形の単元のポイントを紹介します。 のおうぎ形なので、中心角は\(\dfrac{5}{6}\)×360°=300°です。おうぎ形の弧の長さは 中心角に比例 する。 おうぎ形の面積は 中心角に比例 する。 例 中心角が25°のおうぎ形はどれも同じ面積,同じ弧の長さなので, 中心角が2倍の50°になれば面積,弧の長さともに2倍になり, 中心角が3倍の75°になれば面積,弧の長さ
まぁ、これは比を使った考え方を少し応用した公式なので、発想は一緒です。 おうぎ形と円を比べてるわけです。 それでは、どのように使うか実践してみます。 今までと同じ問題 半径3cmで面積が3π㎠のおうぎ形の中心角を求めます。おうぎ形の中心角=360°×底面の半径/母線 円すいの公式2つ(母線=おうぎ形 おうぎ形の面積の求め方2つと葉っぱ(レンズ)形の面積の求め方3つ!等積移動!―「中学受験+塾なし」の勉強法!おうぎ形の中心角を求める問題で,わかっている数字が変わると求め方がわからなくなります。 ※ このQ&Aでは、 「進研ゼミ中学講座」 会員から寄せられた質問とその回答の一部を公開しています。
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ
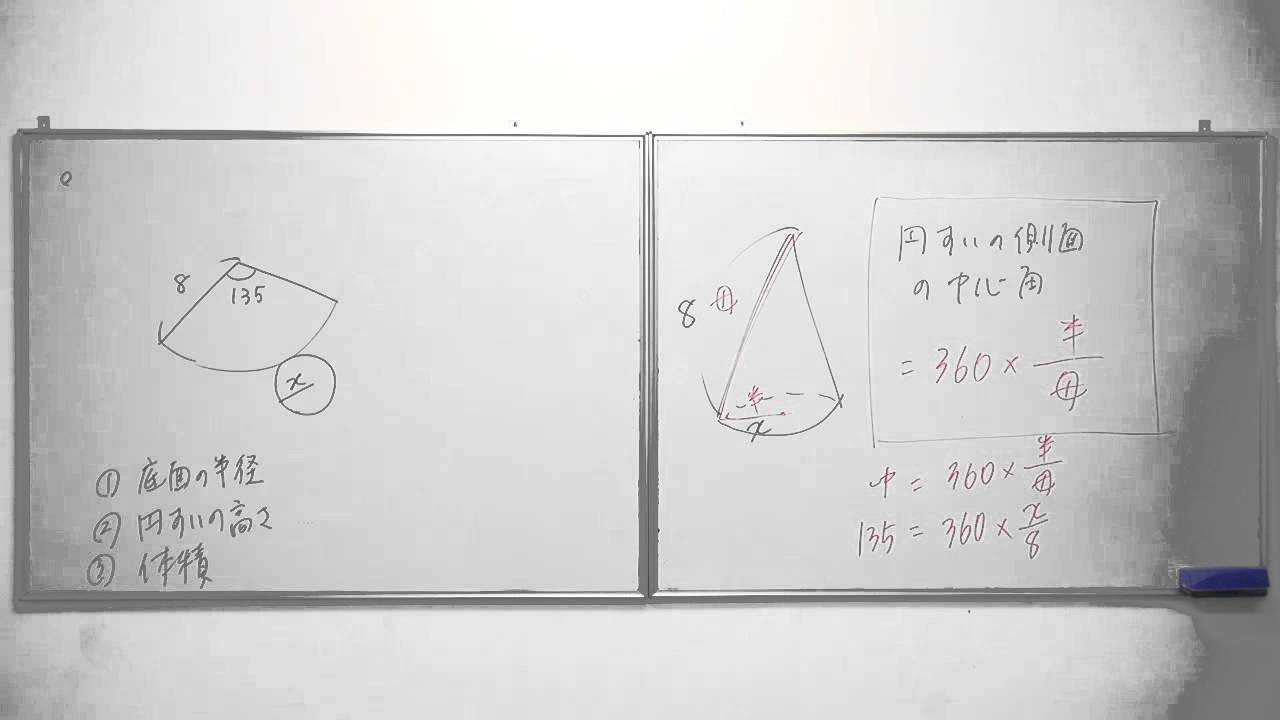 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
数学質問 円すいの側面の中心角の求め方 Youtube
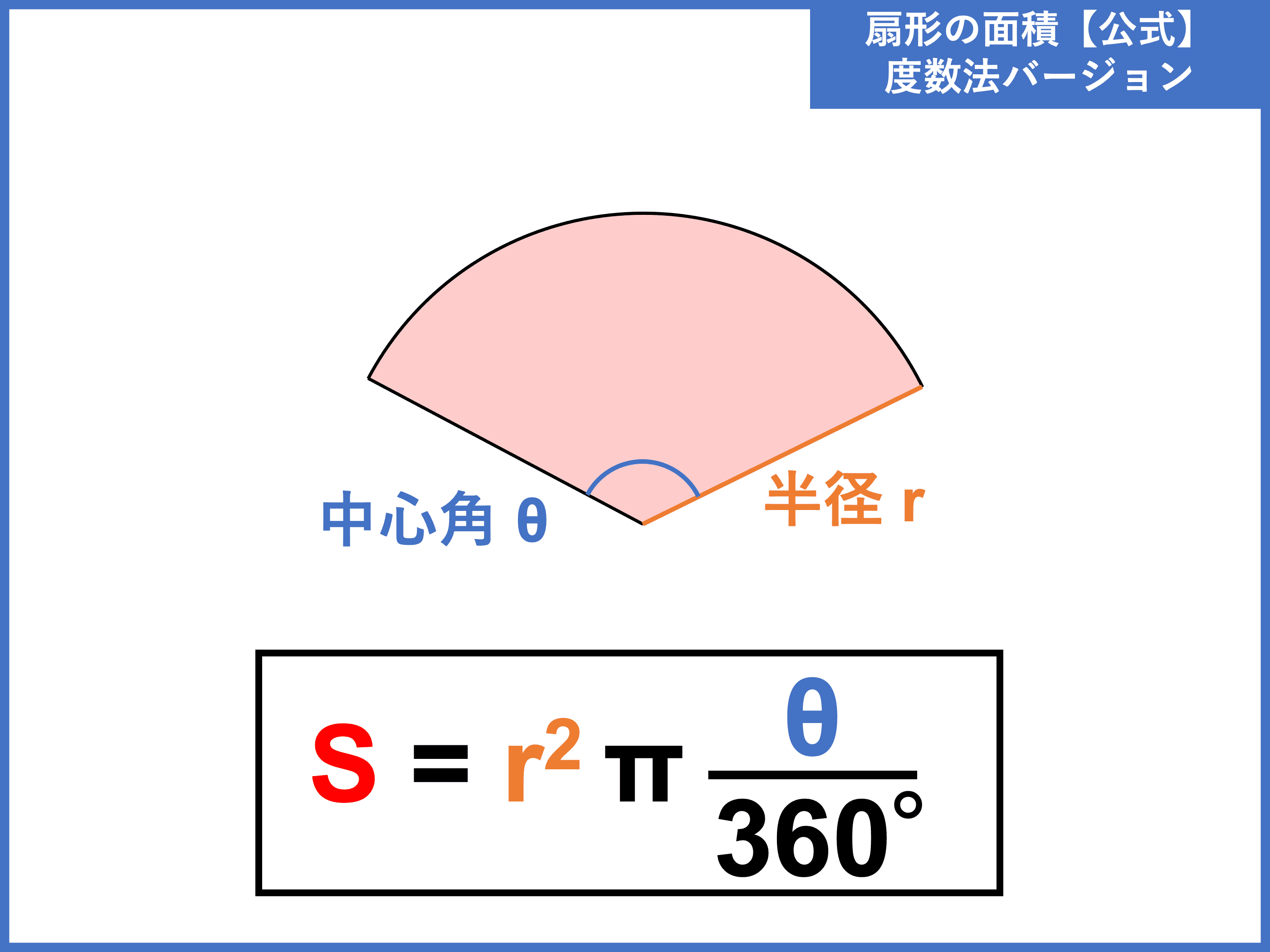
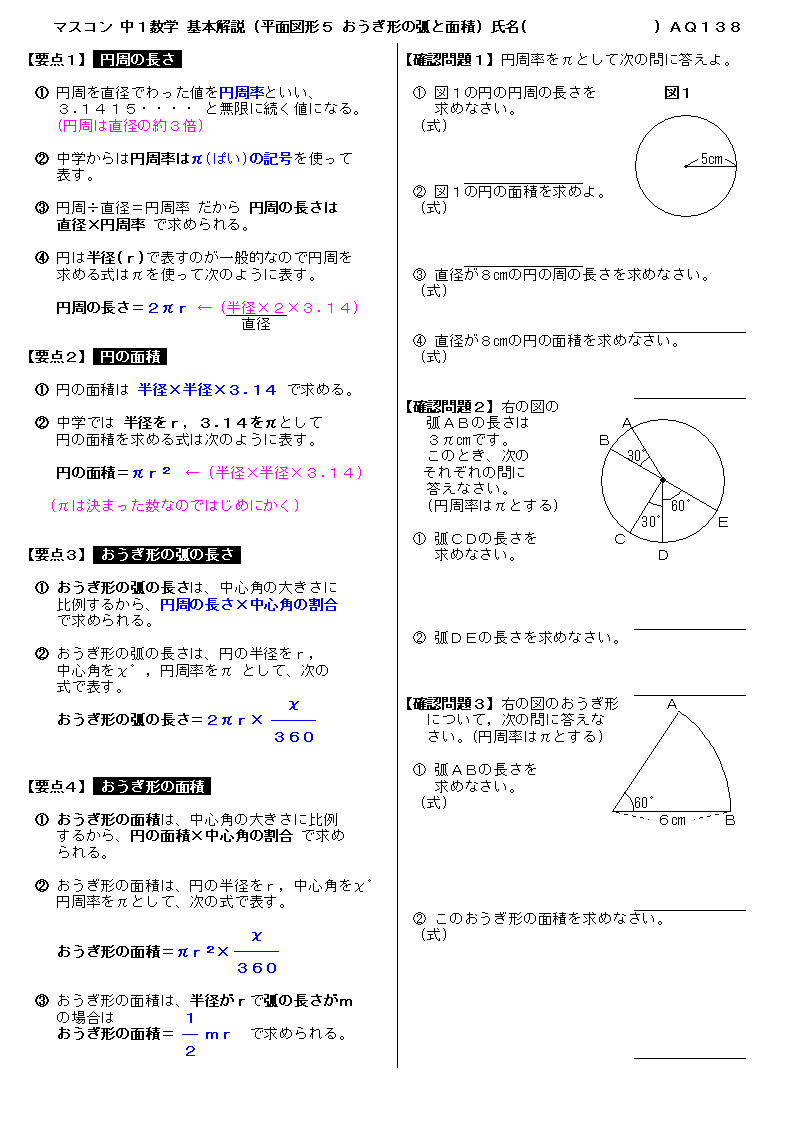
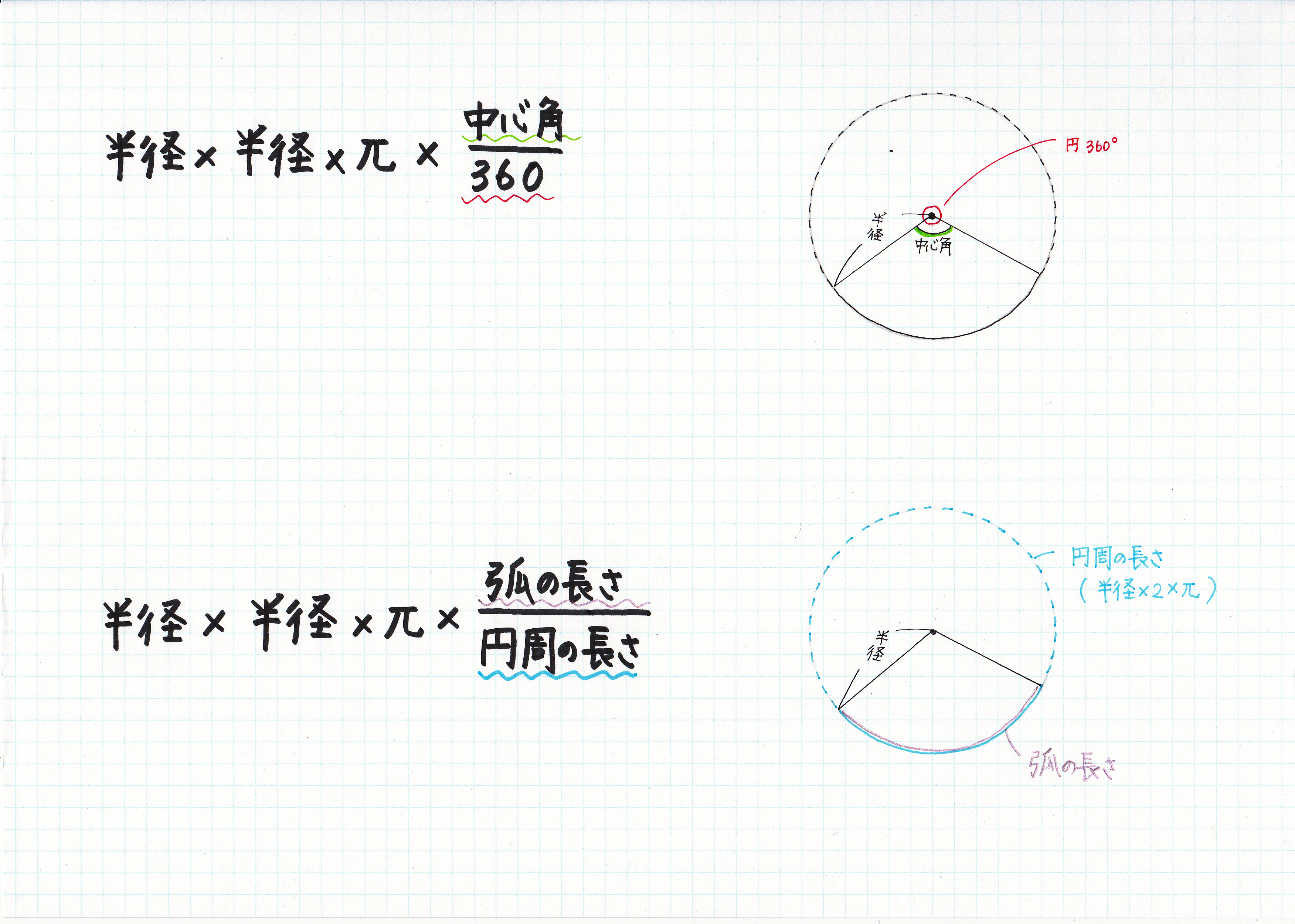
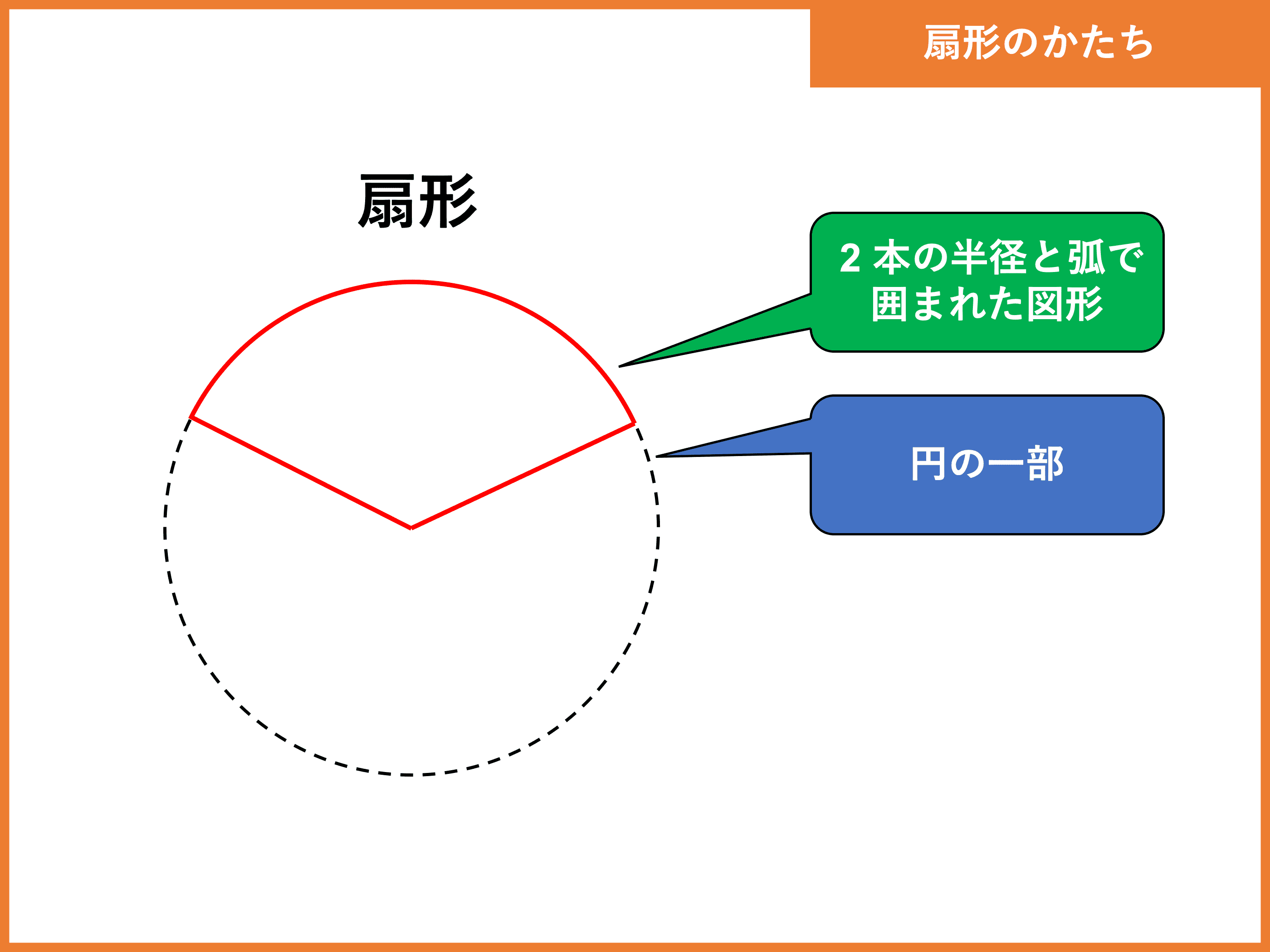
ここがおうぎ形の中心角ですので覚えておきましょう。 中心角を求めよう! 弧の長さの公式を用いた解き方 それでは実際に中心角をどのように求めたらよいのかを見ていきましょう。 弧の長さの公式を用いる中心角の求め方中1の平面図形で習う扇形の問題。 中心角の出し方を3通りの方法で説明します。 通常バージョン まずは通常バージョンから。 公式に当てはめるやり方。教科書にも載っている方法です。 ちょっと面倒くさくて、苦手な生徒も多いこの出し方を説明しよう!③おうぎ形の面積の公式 : πr²× x/360 (半径をr、円周率をπ、中心角をx) これを忘れがちな方は多いですね。 おうぎ形は、円の一部です。円は1周で360度。 そのうちのx度分が知りたいので、 "円の面積の公式 × x/360" となります。
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1です お願いがあります 扇形の中心角の求め方を Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
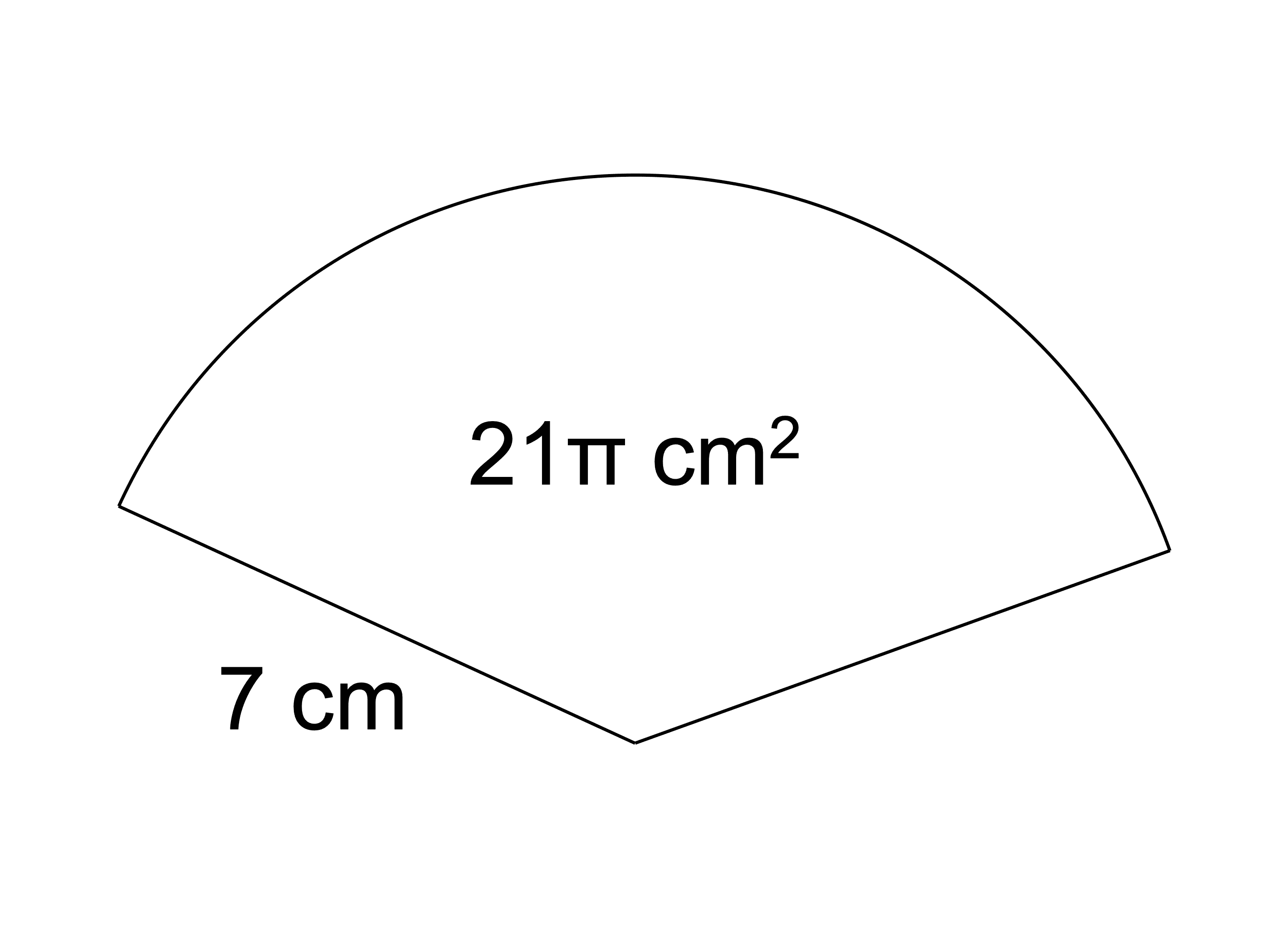
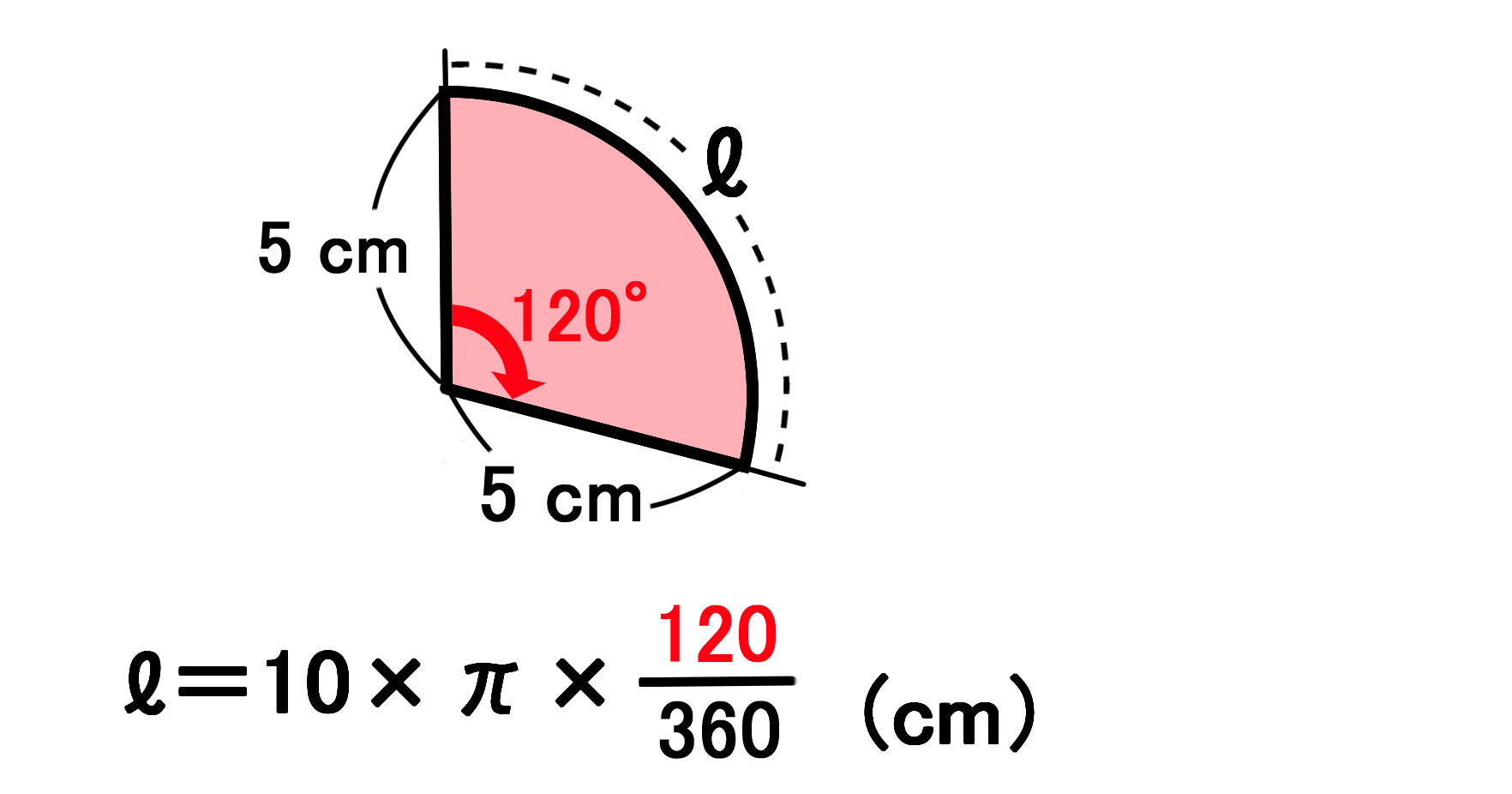
おうぎ形の中心角の求め方 演習問題で理解を深めよう! 円とおうぎ形の公式 まとめ;弧の長さ と 元の円の円周を 比較する このおうぎ形の元になった、 半径 3cm の円 を考えます 半径 3cm の円の 円周の長さ は $\textcolor{red}{直径(半径\times2)\times314}$ より $3\times2\times314=14 cm$ おうぎ型の弧の長さ(問題文より$314cm$)を比べるとおうぎ形の中心角と弧の長さ,中心角と面積の関係について理解する。 ・おうぎ形の面積を公式を利用して求めることができたか。 ・おうぎ形の面積の求め方を確認させる。
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
数学裏ワザ 2 円すいの側面を展開してできるおうぎ形の中心角を一瞬で出す方法を紹介 テストで使える Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
中1の平面図形で習う扇形の問題。 中心角の出し方を3通りの方法で説明します。 通常バージョン まずは通常バージョンから。 公式に当てはめるやり方。教科書にも載っている方法です。 ちょっと面倒くさくて、苦手な生徒も多いこの出し方を説明しよう!おうぎ形の中心角の求め方 演習問題で理解を深めよう! 円とおうぎ形の公式 まとめ;中1数学「平面図形」の5回目は、円とおうぎ形です。基本をしっかり理解すれば、おうぎ形の公式は覚えなくていい。そのことを中心角・弧・面積の求め方半径の求め方円とおうぎ形の複合図形でそれぞれ見ていきましょう。 Part 2 Part 2
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学
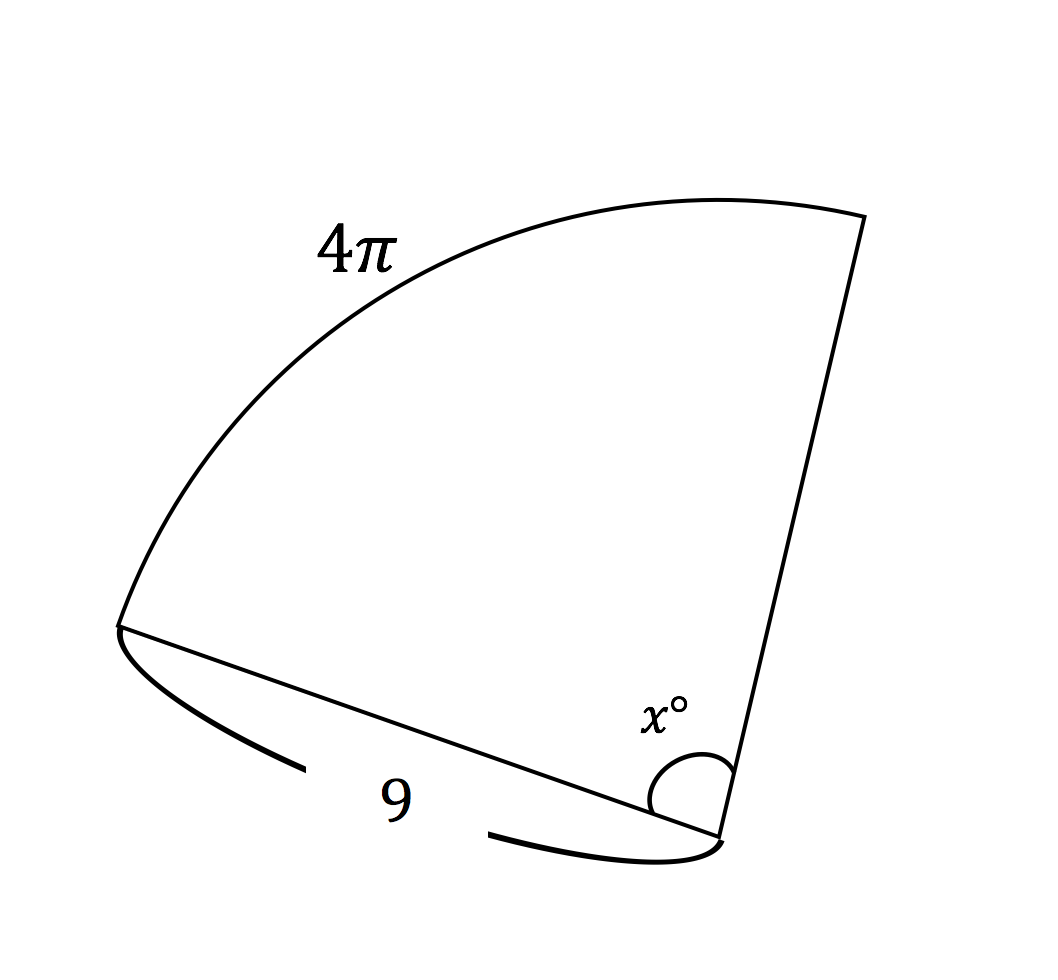
弧の長さ と 元の円の円周を 比較する このおうぎ形の元になった、 半径 3cm の円 を考えます 半径 3cm の円の 円周の長さ は $\textcolor{red}{直径(半径\times2)\times314}$ より $3\times2\times314=14 cm$ おうぎ型の弧の長さ(問題文より$314cm$)を比べると面積の公式を利用して、中心角を求めにいくよ。 中心角をa°とすると、面積の公式は、 (おうぎ形の面積)=(半径)×(半径)×π×a°/360° ここに具体的な数を入れると、 50π=10×10×π×a°/360° 方程式を解けば、中心角が求められるね。中心角を \(x\) とすると、問題文から弧の長さが与えられているので $$2\times \pi \times 3\times \frac{x}{360}=3\pi$$ という方程式を作ることができます。 まずは両辺から\(\pi\)を消し、左辺を約分します。 $$\frac{x}{60}=3$$ 両辺に×60して、中心角の値を求めます。
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
印刷可能無料 平面図形 おうぎ形 Fuutou Sozai
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
作図 角度15 30 45 60 75 90 105 の作り方を解説 数スタ
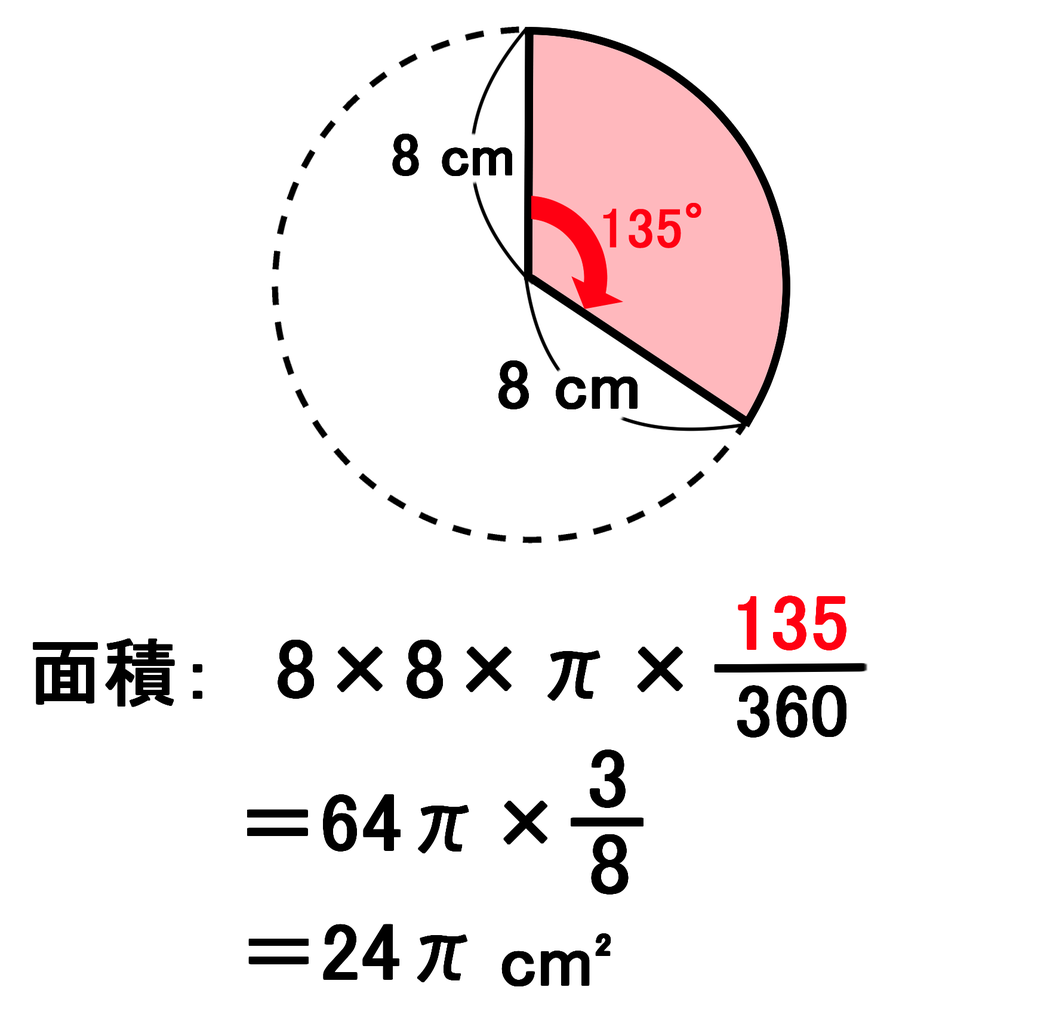
半径3cm,中心角1°のおうぎ形の面積と弧の長さを求めなさい。 問題の見方 半径と中心角を,おうぎ形の公式に代入して求めましょう。 この公式が覚えづらい人は,おうぎ形が円の一部だということを意識しましょう。公式をつかわない!扇形の中心角の求め方3つのステップ それじゃあ、なぜこの公式で扇形の中心角が求められるのか?? ちょっと気になるよね?? じつは、扇形の中心角の公式は、 比例式をつかった中心角の求め方 から導きだしたものなんだ。おうぎ形の弧の長さは 中心角に比例 する。 おうぎ形の面積は 中心角に比例 する。 例 中心角が25°のおうぎ形はどれも同じ面積,同じ弧の長さなので, 中心角が2倍の50°になれば面積,弧の長さともに2倍になり, 中心角が3倍の75°になれば面積,弧の長さ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
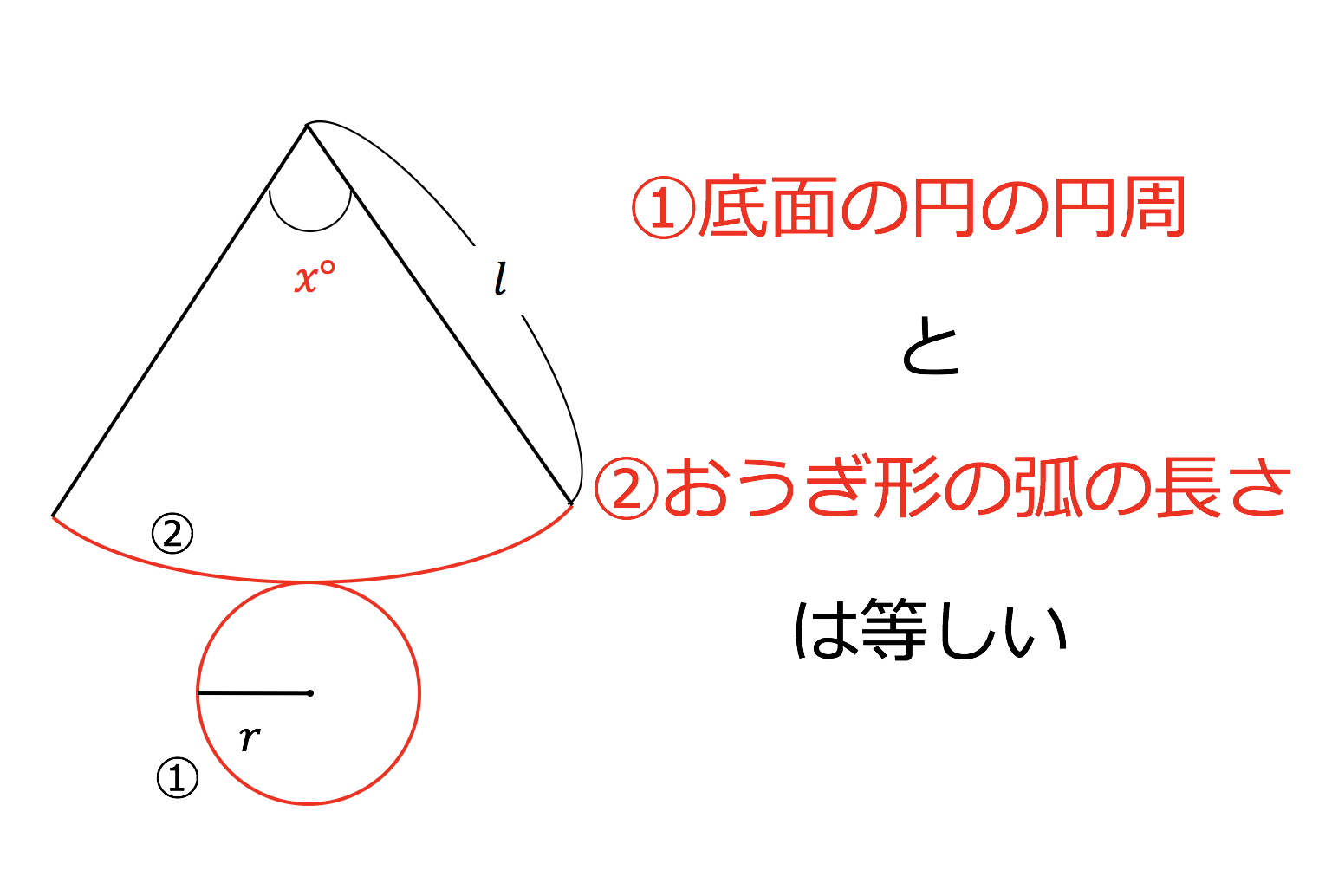
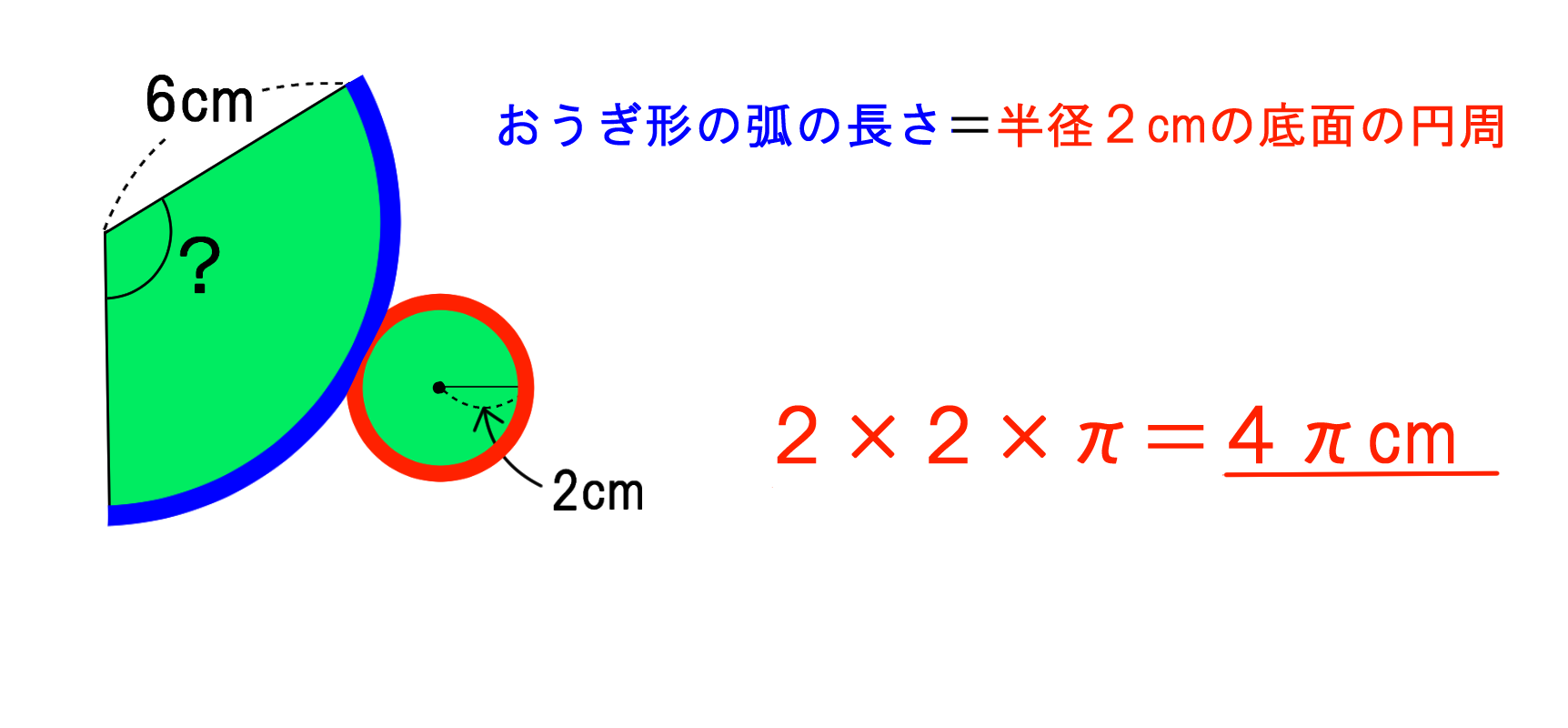
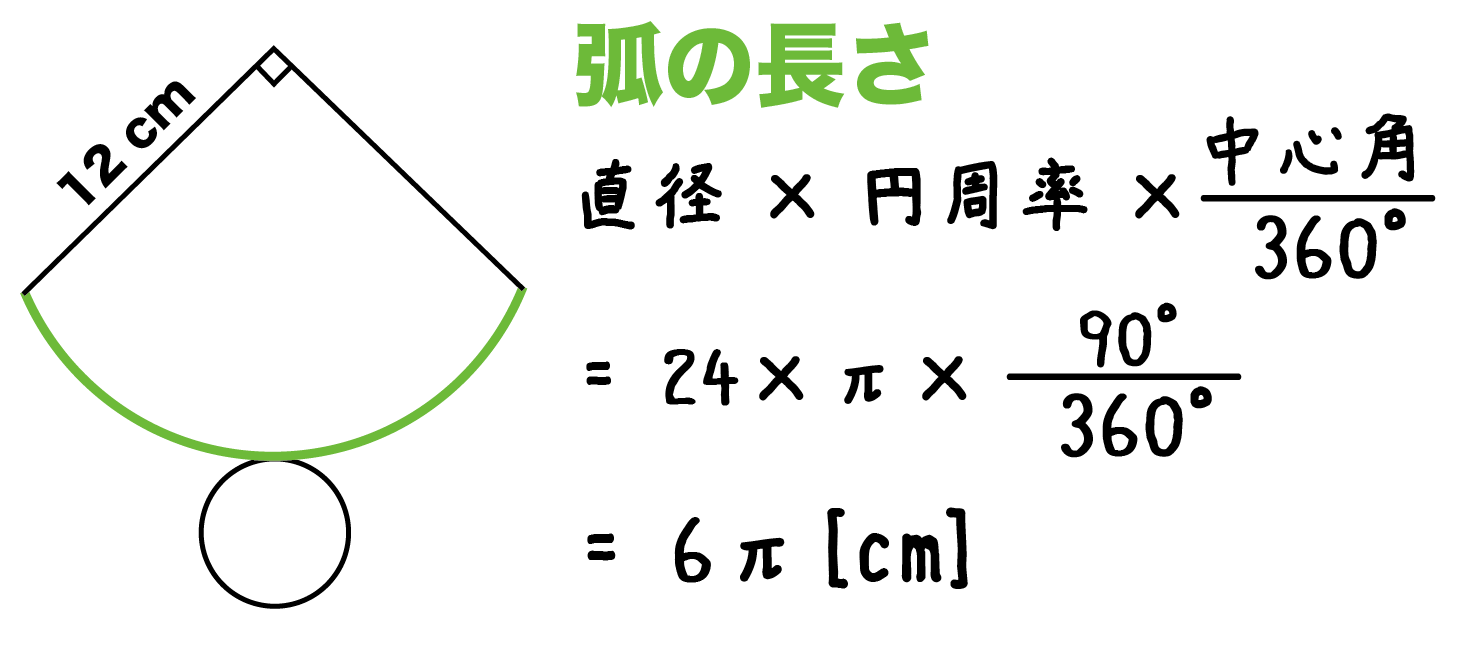
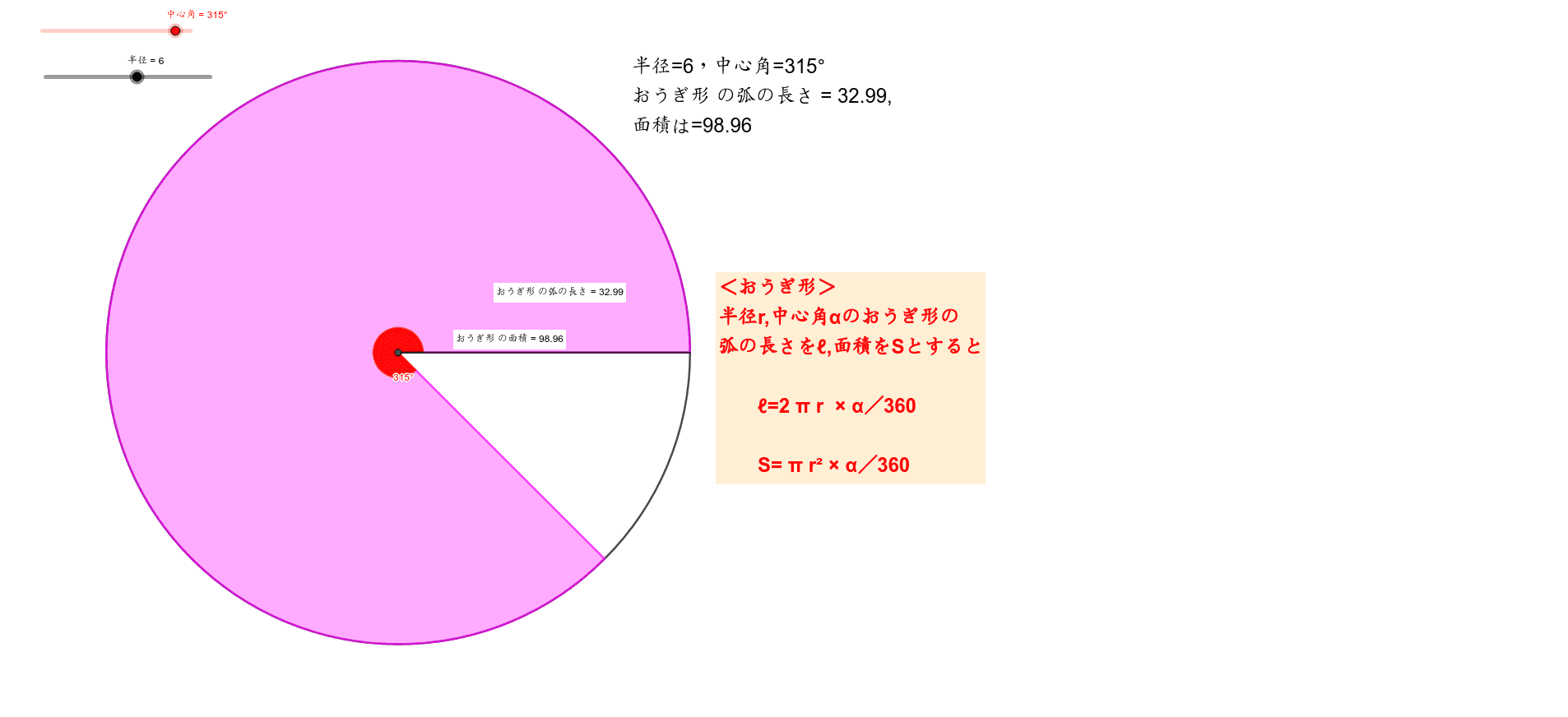
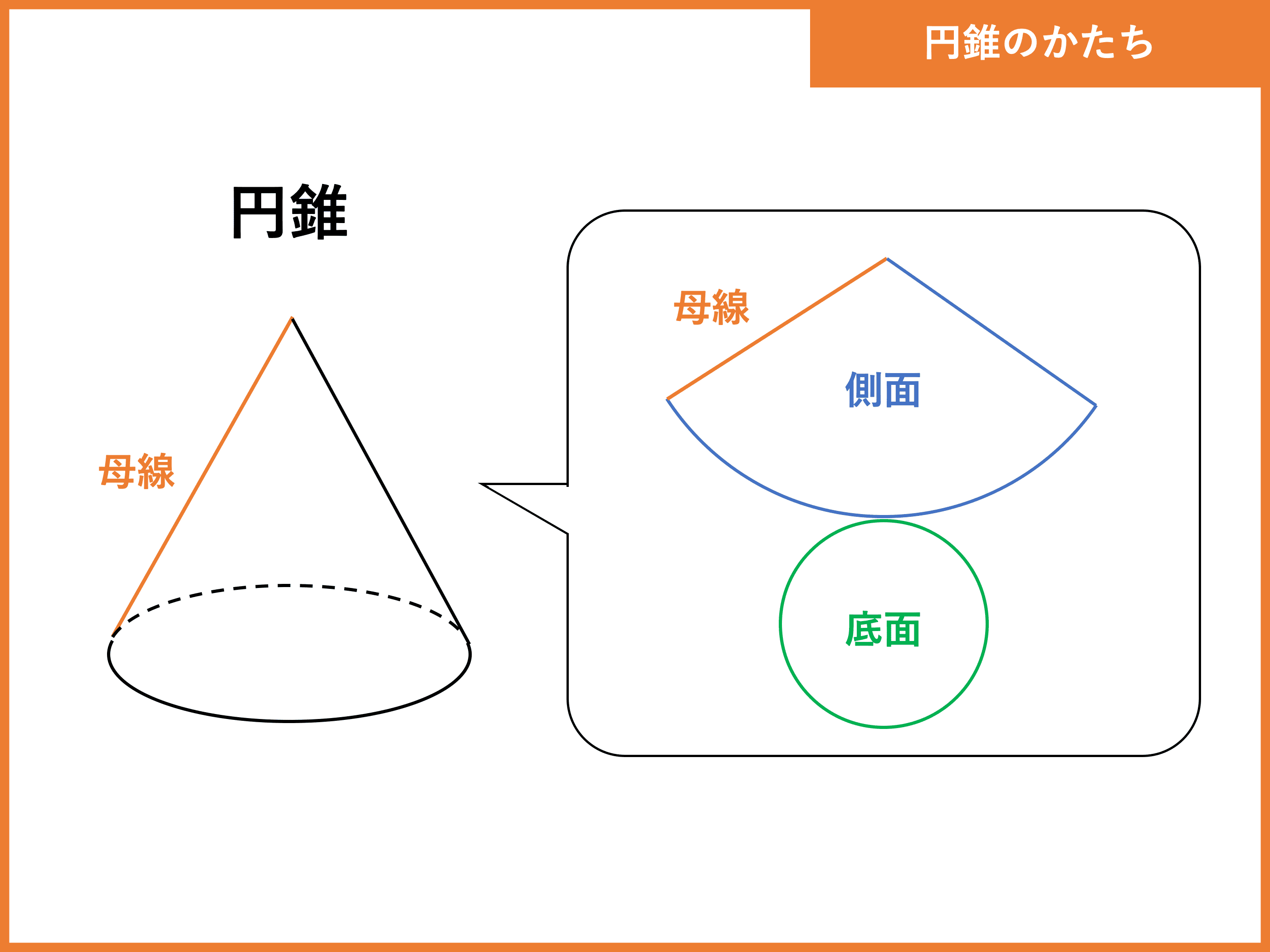
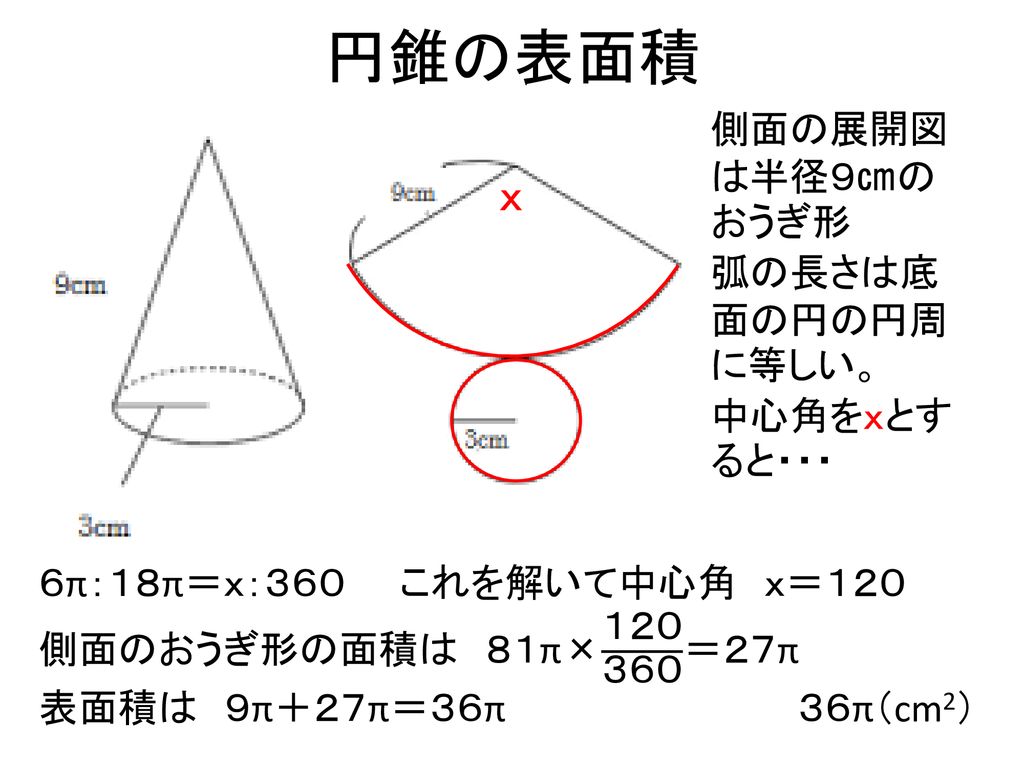
おうぎ形の面積の求め方2 もう一つのおうぎ形の面積の求め方は円の面積を求めてから、そこから中心角を用いておうぎ形を求める方法です。 まずは簡単におうぎ形の中心角が $60^{\circ}$ の場合を考えます。おうぎ形の面積が (cm 2)、中心角が 1°の円の半径を求めてください。ただし円周率を 314とします。 おうぎ形の面積を求める公式は \ おうぎ形の面積 = 円の面積 \times \frac{中心角}{360°} \ なので、円の半径を \(r\) とすると(1) 展開図のおうぎ形の中心角を求めなさい。 (2) 円すいの側面積を求めなさい。 (3) 円すいの表面積を求めなさい。 基本の考え方 円すいの展開図では、側面がおうぎ形、底面が円となりますので、 「おうぎ形の弧の長さ=底面の円周」 に着目します。
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
(1) 展開図のおうぎ形の中心角を求めなさい。 (2) 円すいの側面積を求めなさい。 (3) 円すいの表面積を求めなさい。 基本の考え方 円すいの展開図では、側面がおうぎ形、底面が円となりますので、 「おうぎ形の弧の長さ=底面の円周」 に着目します。中1の平面図形で習う扇形の問題。 中心角の出し方を3通りの方法で説明します。 通常バージョン まずは通常バージョンから。 公式に当てはめるやり方。教科書にも載っている方法です。 ちょっと面倒くさくて、苦手な生徒も多いこの出し方を説明しよう!おうぎ形の面積が (cm 2)、中心角が 1°の円の半径を求めてください。ただし円周率を 314とします。 おうぎ形の面積を求める公式は \ おうぎ形の面積 = 円の面積 \times \frac{中心角}{360°} \ なので、円の半径を \(r\) とすると
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Msワードで中心角がわかっているおうぎ形 Wordで数学問題プリントを作ろう
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形の面積の便利公式 中学1年数学 Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
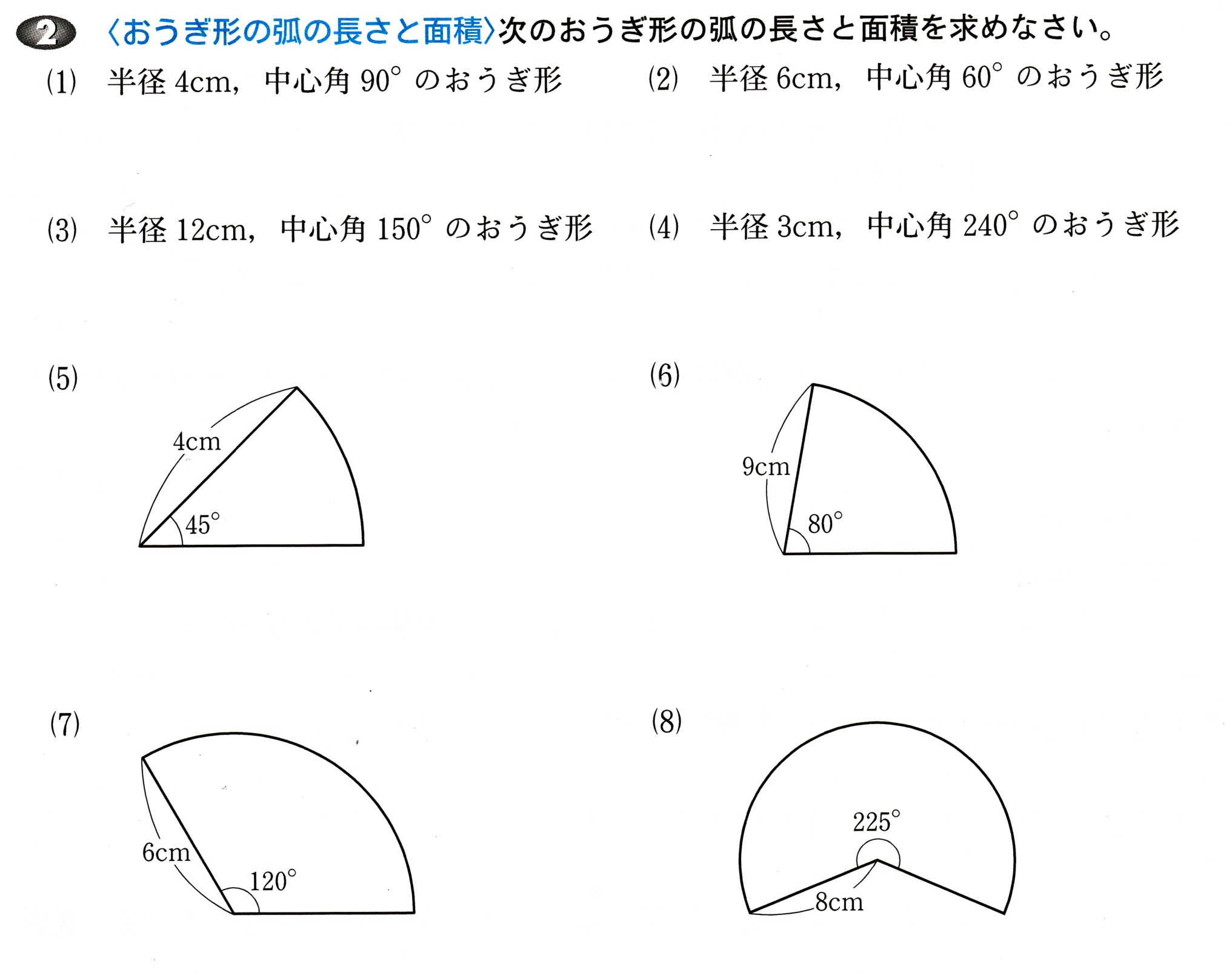
無料 中1数学 基本解説 問題プリント 平面図形5 おうぎ形の弧と面積 138
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形 注意 周りの長さを求める公式を解説 数スタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
灘中模試 No 029 平面図形 算数星人のweb問題集 中学受験算数の問題に挑戦
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1数学 円すいの問題 練習編 映像授業のtry It トライイット
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
計算公式 円錐の表面積の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中学1年数学 円とおうぎ形の計算 練習問題2 あんのん塾
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形の弧の長さと面積 Ppt Download
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1数学 おうぎ形の中心角の求め方 家庭教師のガンバ Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中心角の求め方が即わかる 合わせて知りたい知識とは 高校生向け受験応援メディア 受験のミカタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Http Www Tochusu Com Kyoikukatei 15 Kyoiku Pdf
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中学数学 円錐の高さの求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
โน ตของ 中1数学 おうぎ形のポイント ช น Junior High数学 Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形の面積の公式について 現役塾講師のわかりやすい中学数学の解き方
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Studydoctorおうぎ形の公式と忘れない考え方 中学1年数学 Studydoctor
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
簡単作図 円錐の展開図の書き方がわかる4つのステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
2 の求め方がわかりません S 1 2lr Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
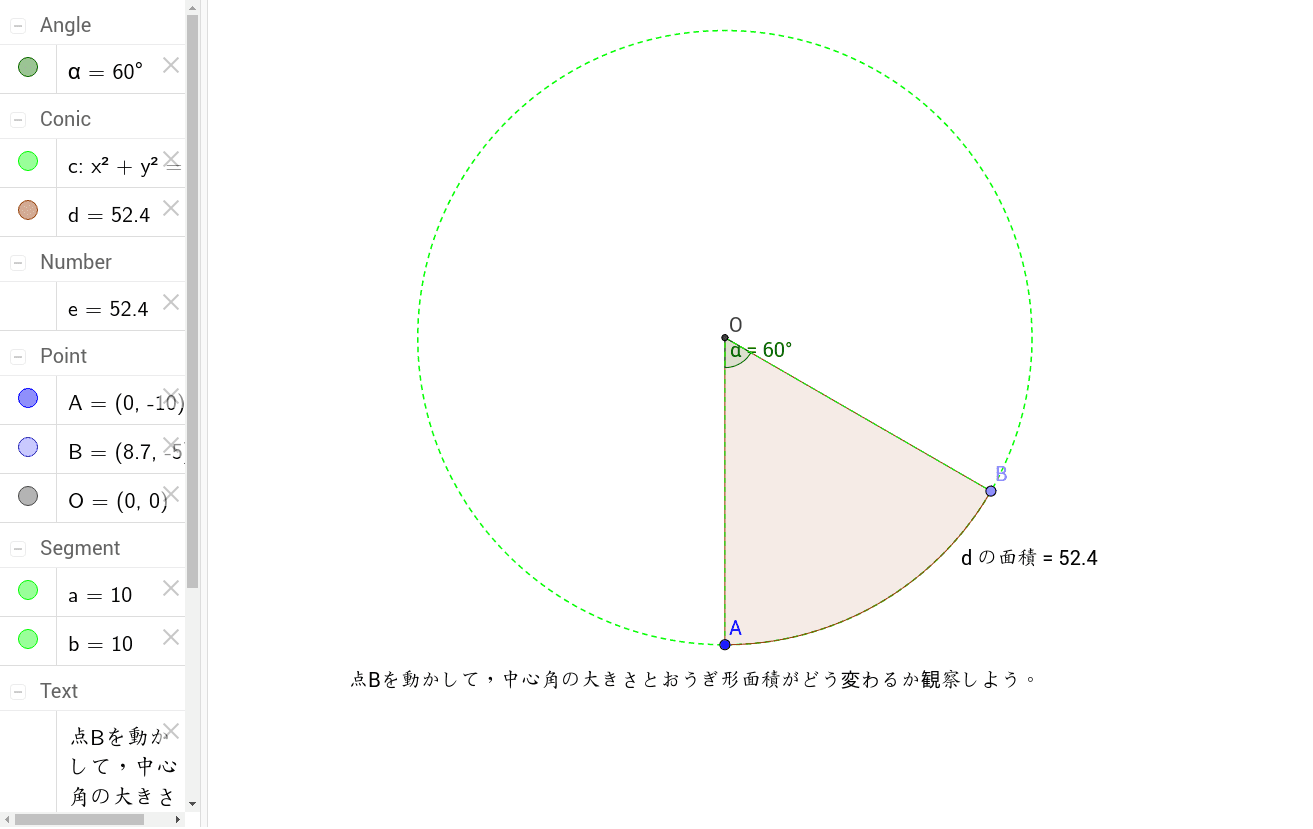
中1 おうぎ形の弧の長さや面積について考えよう Geogebra
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1数学 円すいの問題 練習編 映像授業のtry It トライイット
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形の面積と弧の長さの求め方 バカでもわかる 中学数学
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Msワードでおうぎ形の利用 Wordで数学問題プリントを作ろう
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Kids Gakken Co Jp Box Sansu 05 Pdf B Pdf
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形とは 面積 中心角 半径 弧の長さの公式と求め方 受験辞典
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形 中心角の求め方を公式を用いて解説するぞ Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
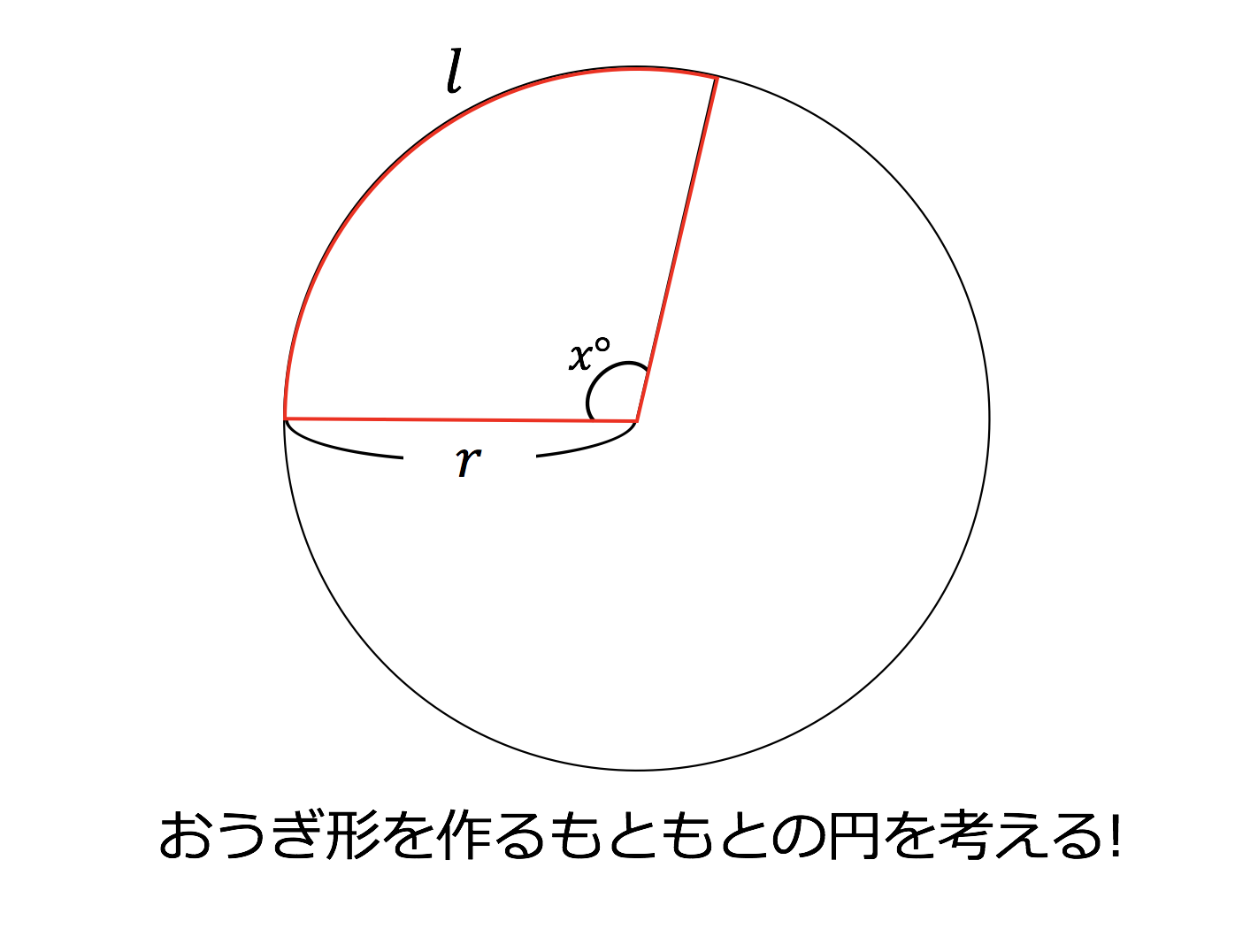
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
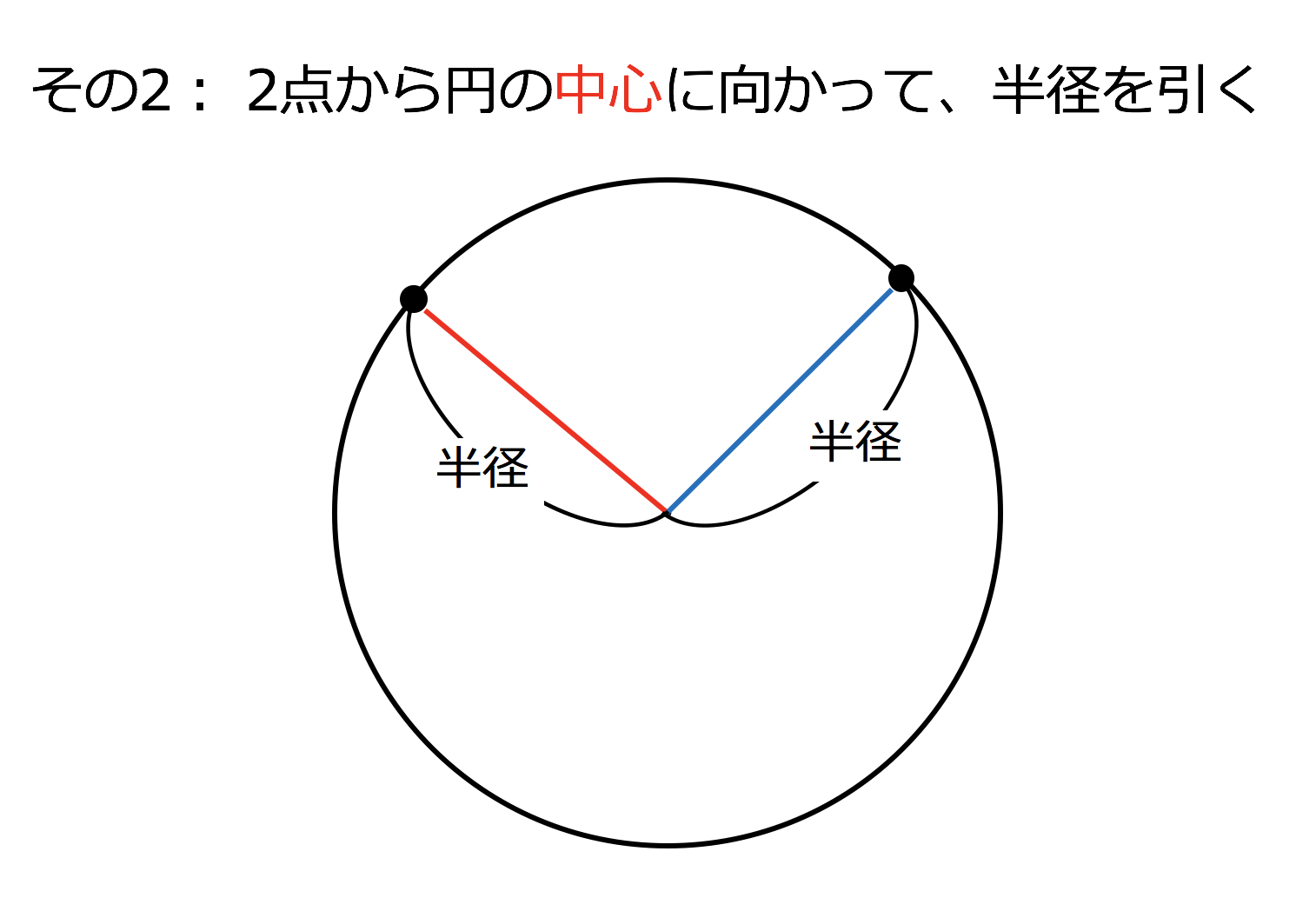
中1数学 おうぎ形の中心角の求め方 について ひっそりと物理や数学を解説する
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
この問題の式の2pって 直径を求めるの12 2の2 半径 2 Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
円錐の表面積 中心角を求める問題を丁寧に解説 数スタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
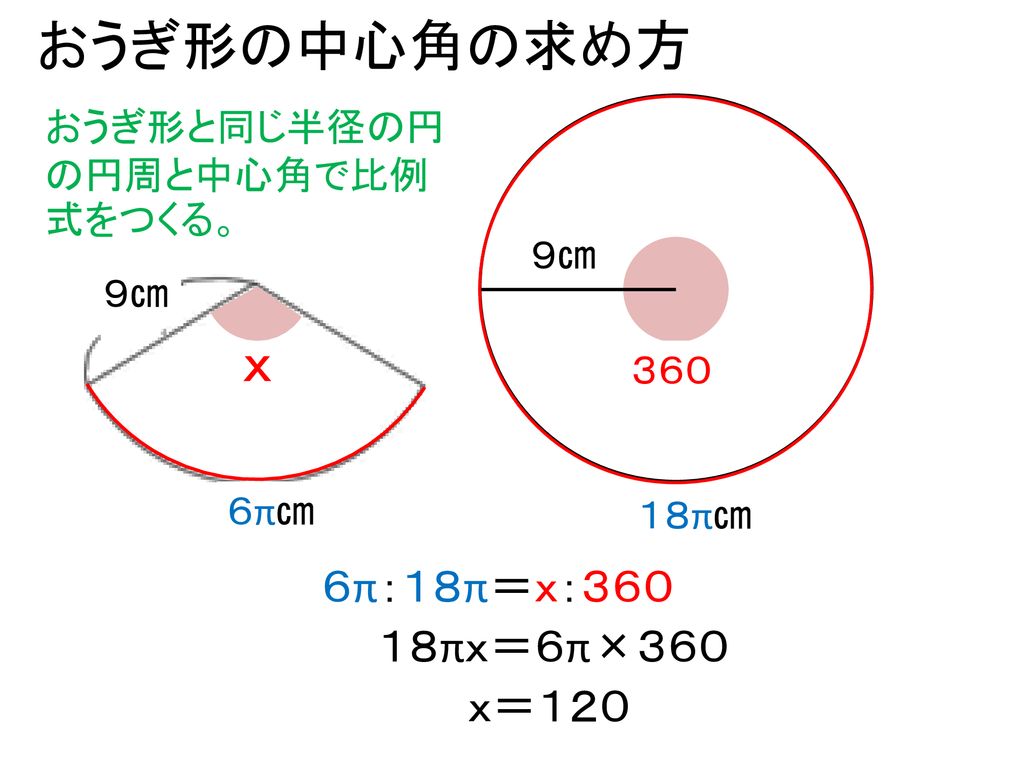
本時の目標 いろいろな立体の表面積を求めることができる Ppt Download
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
2分でわかる 扇形 おうぎ形 の弧の長さの求め方 Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
カンタン公式 扇形の中心角の求め方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
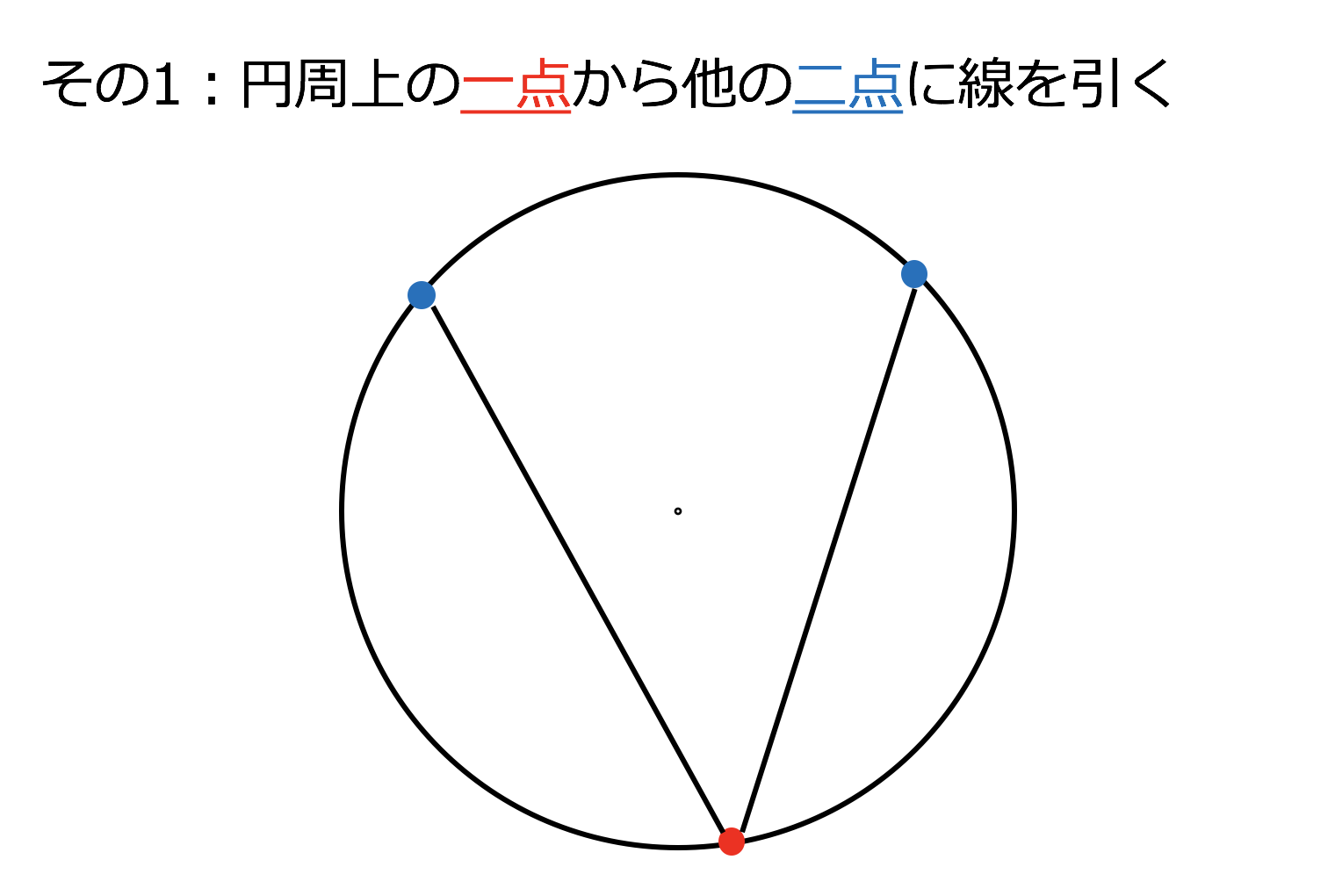
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1 数学 範囲 円とおうぎ形の計量 大放出ぅ 中学生 数学のノート Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形 中心角を求める3つのパターンを解説 方程式で解く 比を使う 数スタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Http S Ir Sap Hokkyodai Ac Jp Dspace Bitstream 1 69 2 Kyoiku 14 Pdf
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
半径6cm 弧の長さ2pcmのおうぎがたの面積 はどーやって求めますか Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1 円とおうぎ形の計量 おうぎ形の面積 日本語版 Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ型の計算 中学数学に関する質問 勉強質問サイト
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
โน ตของ 中1 数学 範囲 おうぎ形の中心角の求め方 大放出ぅ Clear
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
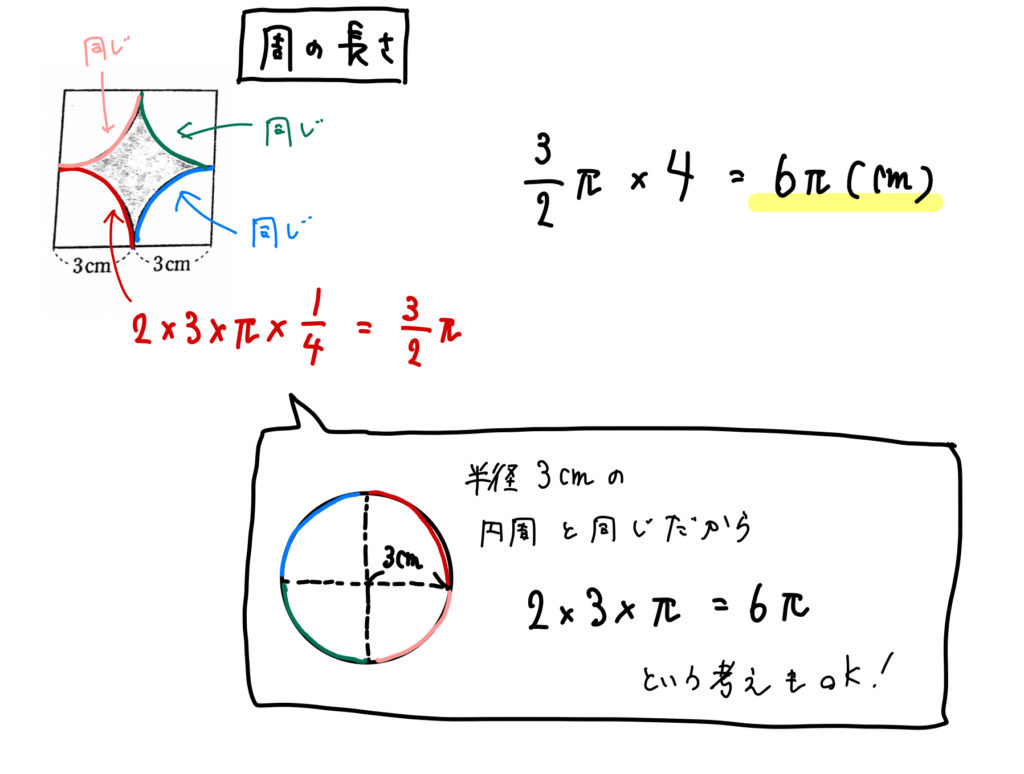
おうぎ形の応用 影の部分の面積 周の長さの求め方 数スタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
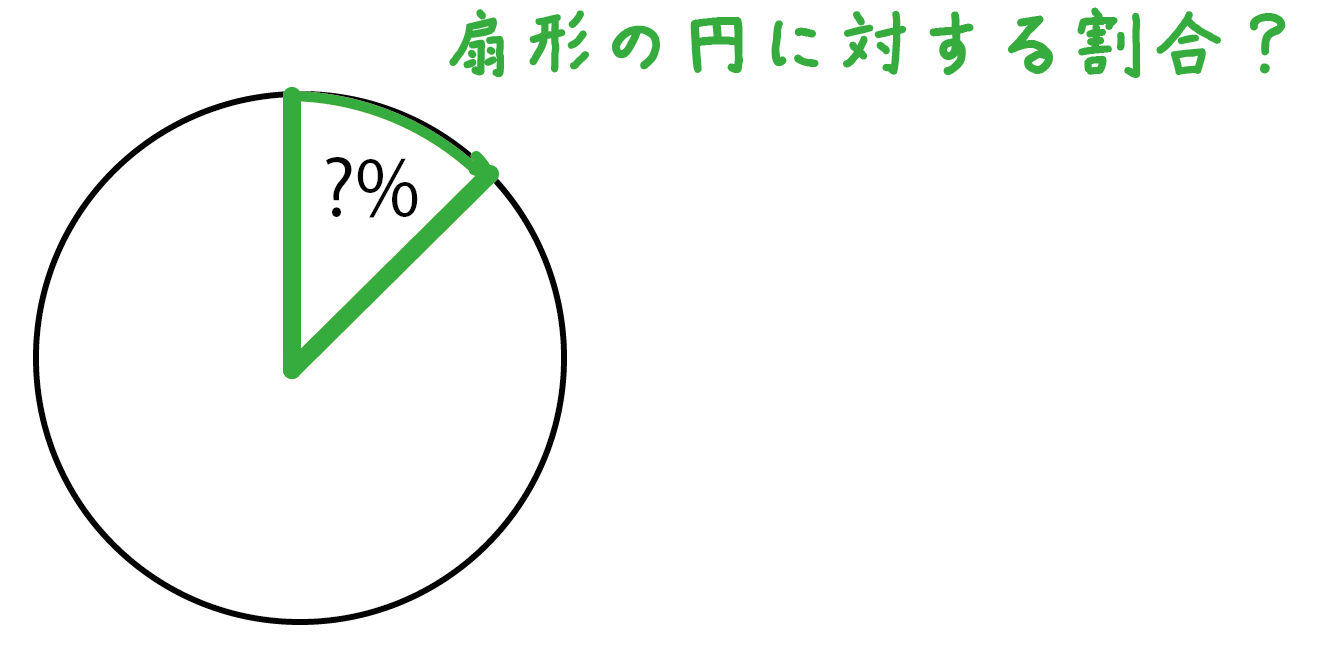
扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
壁紙 押入れ 無料ダウンロード 扇 面積 求め 方
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
3分で分かる 中心角の求め方ー公式とその証明 練習問題をわかりやすく 合格サプリ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
高校受験数学 円とおうぎ形 中心角の求め方 方程式編の授業映像 プリント無料配布 Youtube スタディカフェ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
5ステップでわかる 底面が扇形の立体の表面積の求め方 Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
本時の目標 いろいろな立体の表面積を求めることができる Ppt Download
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
おうぎ形 面積 弧の長さ 中心角の求め方を問題解説 数スタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形の公式は暗記しない 割合という考え方を導入するだけでスラスラ解ける 中学受験ナビ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
図形 は半径2 中心角60 のおうぎ形を3つ重ねたものです Yahoo 知恵袋
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1 数学 中1 75 おうぎ形の弧と面積 基本編 Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
高校受験数学 円とおうぎ形 中心角の求め方 方程式編の授業映像 プリント無料配布 Youtube スタディカフェ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
扇形の面積公式が一目でわかる 丁寧な証明付き 高校生向け受験応援メディア 受験のミカタ
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
簡単公式 円錐の側面積の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中1 数学 空間図形9 おうぎ形の公式 17分 Youtube
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
印刷可能無料 平面図形 おうぎ形 Fuutou Sozai
 Performance & security by Cloudflare
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
中学数学 3分で簡単にわかる 扇形 おうぎ形 の面積の求め方 の公式 Qikeru 学びを楽しくわかりやすく
 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式" />
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式" />  Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 



 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 



 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 



 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 

 Performance & security by Cloudflare おうぎ形 中心角 求め方 公式">
Performance & security by Cloudflare おうぎ形 中心角 求め方 公式"> 



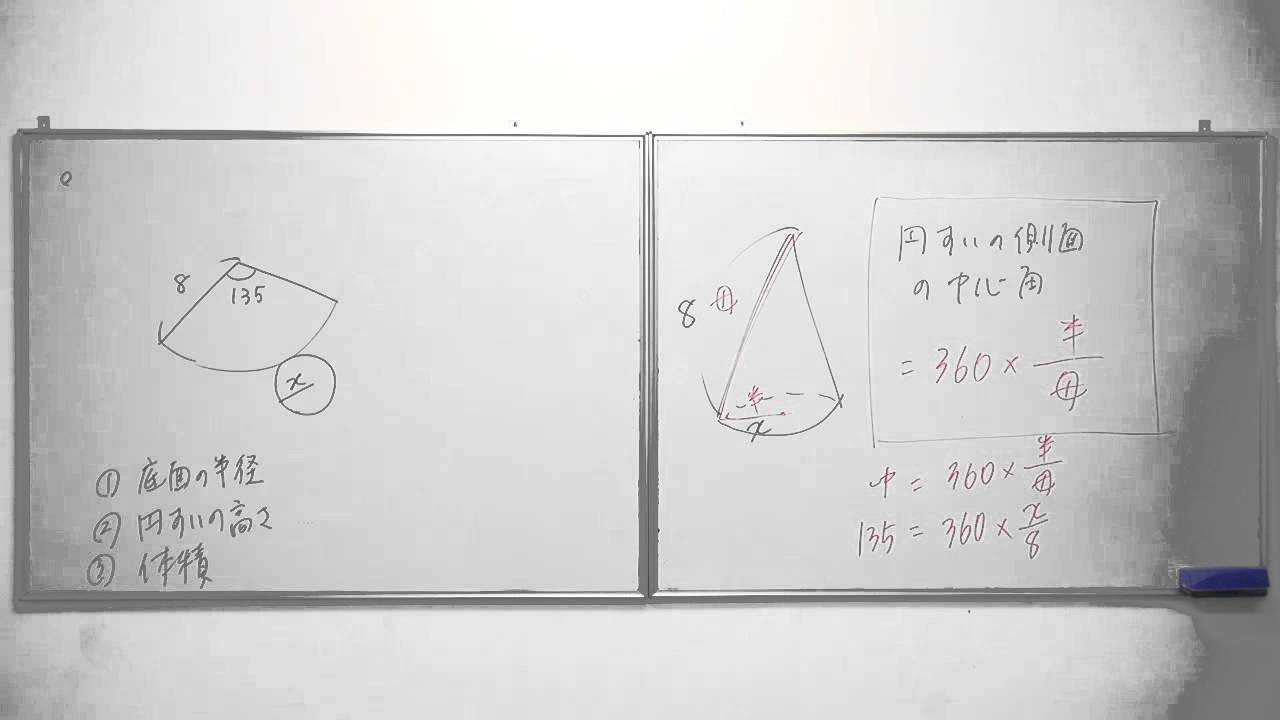












































































コメント
コメントを投稿